As someone deeply immersed in the world of finance and accounting, I often find myself exploring theories that explain how individuals make decisions about saving and spending. One such theory that has profoundly influenced my understanding is the Life Cycle Hypothesis (LCH). Developed by Franco Modigliani and his student Richard Brumberg in the 1950s, the LCH provides a framework for understanding how people plan their consumption and savings over their lifetime. In this article, I will delve into the intricacies of the Life Cycle Hypothesis, explore its mathematical foundations, and discuss its relevance in the context of the US economy.
Table of Contents
What Is the Life Cycle Hypothesis?
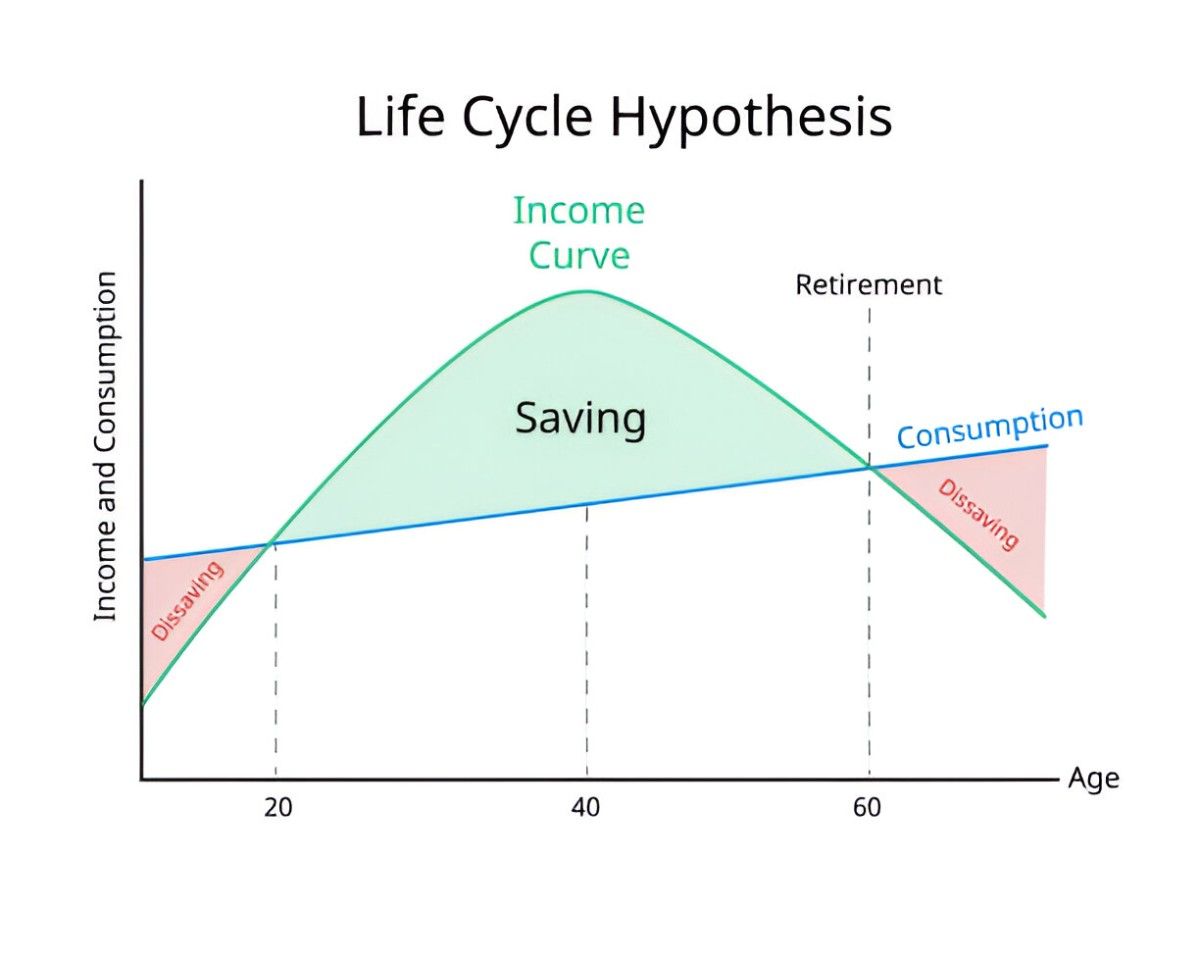
The Life Cycle Hypothesis posits that individuals plan their consumption and savings behavior based on their expected lifetime income rather than their current income. In other words, people smooth their consumption over their lifetime, saving during their working years and dissaving during retirement. This theory challenges the traditional Keynesian view, which suggests that consumption is primarily a function of current income.
From my perspective, the LCH makes intuitive sense. Think about it: when you start your career, your income might be modest, but you expect it to grow over time. During your peak earning years, you save a portion of your income to support yourself in retirement when your income drops. This behavior aligns with the LCH’s core idea of consumption smoothing.
The Mathematical Foundation of the Life Cycle Hypothesis
To understand the LCH more deeply, let’s explore its mathematical underpinnings. The hypothesis can be expressed using the following equation:
C = \frac{W + R \cdot Y}{T}Where:
- C represents annual consumption.
- W is the initial wealth.
- R is the number of remaining working years.
- Y is the annual income.
- T is the total lifespan in years.
This equation shows that consumption is a function of both wealth and income, spread over an individual’s lifetime. Let’s break it down with an example.
Example: Calculating Consumption Using the LCH
Suppose John is 30 years old, plans to retire at 65, and expects to live until 85. He has an initial wealth of $50,000 and earns $60,000 annually. Using the LCH formula, we can calculate his annual consumption:
C = \frac{50,000 + 35 \cdot 60,000}{55} = \frac{50,000 + 2,100,000}{55} = \frac{2,150,000}{55} = 39,090.91John’s annual consumption, according to the LCH, would be approximately $39,091. This means he would save a portion of his income during his working years to maintain this level of consumption during retirement.
The Role of Savings in the Life Cycle Hypothesis
Savings play a critical role in the LCH. During their working years, individuals save a portion of their income to build a nest egg for retirement. This behavior can be represented mathematically as:
S = Y - CWhere:
- S represents savings.
- Y is the annual income.
- C is the annual consumption.
Using John’s example, his annual savings would be:
S = 60,000 - 39,091 = 20,909John saves approximately $20,909 annually during his working years. These savings accumulate over time, providing him with financial security during retirement.
The Life Cycle Hypothesis and Retirement
Retirement is a pivotal phase in the LCH. During this period, individuals rely on their accumulated savings to maintain their standard of living. The amount of savings required for retirement can be calculated using the following formula:
W_r = S \cdot RWhere:
- W_r represents the wealth required for retirement.
- S is the annual savings.
- R is the number of working years.
Continuing with John’s example, his required retirement wealth would be:
W_r = 20,909 \cdot 35 = 731,815John needs to accumulate approximately $731,815 by the time he retires to maintain his annual consumption of $39,091 during retirement.
The Impact of Interest Rates on the Life Cycle Hypothesis
Interest rates influence the LCH by affecting the returns on savings and the cost of borrowing. Higher interest rates encourage saving, as individuals earn more on their investments. Conversely, lower interest rates may discourage saving and encourage borrowing.
The present value of lifetime income can be calculated using the following formula:
PV = Y \cdot \frac{1 - (1 + r)^{-R}}{r}Where:
- PV represents the present value of lifetime income.
- Y is the annual income.
- r is the interest rate.
- R is the number of working years.
Let’s assume an interest rate of 5% for John’s case:
PV = 60,000 \cdot \frac{1 - (1 + 0.05)^{-35}}{0.05} = 60,000 \cdot \frac{1 - 0.181}{0.05} = 60,000 \cdot 16.38 = 982,800The present value of John’s lifetime income is approximately $982,800. This calculation helps individuals understand how much they need to save to achieve their retirement goals.
The Life Cycle Hypothesis in the US Context
The LCH has significant implications for the US economy, particularly in light of demographic trends such as an aging population and increasing life expectancy. According to the US Census Bureau, the number of Americans aged 65 and older is projected to nearly double from 52 million in 2018 to 95 million by 2060. This demographic shift underscores the importance of saving for retirement.
Moreover, the LCH highlights the role of social security and pension systems in supporting consumption during retirement. In the US, Social Security benefits provide a safety net for retirees, but they are often insufficient to maintain pre-retirement living standards. This gap necessitates personal savings and investments.
Criticisms and Limitations of the Life Cycle Hypothesis
While the LCH provides a robust framework for understanding consumption and saving behavior, it is not without its limitations. One criticism is that it assumes individuals have perfect foresight and can accurately predict their lifetime income and expenses. In reality, factors such as job loss, health issues, and economic downturns can disrupt these plans.
Additionally, the LCH assumes that individuals are rational and make decisions solely based on economic considerations. However, behavioral economics has shown that psychological factors, such as procrastination and present bias, can influence saving behavior.
Comparing the Life Cycle Hypothesis with Other Theories
To gain a holistic understanding, it’s helpful to compare the LCH with other economic theories. For instance, the Permanent Income Hypothesis (PIH), developed by Milton Friedman, also emphasizes consumption smoothing but focuses on permanent income rather than lifetime income. While the LCH considers the entire lifespan, the PIH distinguishes between permanent and transitory income.
Another relevant theory is the Keynesian Consumption Function, which posits that consumption is primarily a function of current income. Unlike the LCH, this theory does not account for future income expectations or the role of savings in smoothing consumption.
Practical Applications of the Life Cycle Hypothesis
The LCH has practical applications in personal finance, retirement planning, and public policy. For individuals, it underscores the importance of saving early and consistently to achieve financial security in retirement. Financial advisors often use the LCH to develop personalized retirement plans for their clients.
From a policy perspective, the LCH highlights the need for robust social security systems and incentives for retirement savings. Policymakers can use the LCH to design programs that encourage saving and address the challenges posed by an aging population.
Conclusion
The Life Cycle Hypothesis offers a compelling framework for understanding how individuals plan their consumption and savings over their lifetime. By emphasizing the importance of lifetime income and consumption smoothing, the LCH provides valuable insights into personal finance and retirement planning. While it has its limitations, the LCH remains a cornerstone of economic theory, with significant implications for individuals and policymakers alike.